Intertemporal trade and Current Account balances (Model With Investment)
Historically, one of the main reasons countries have borrowed abroad is to finance productive investments that would have been hard to finance out of domestic savings alone. In the previous article, we discussed the consumption smoothing of the current account, identifying the current account with national savings. In general, however, the current account equals saving minus investment. And because, in reality, investment usually is much more volatile than saving, to ignore investment is to miss a lot.
In this model, we assume that output is produced using capital, which, in turn, can be accumulated through investment. The production function for new output in either period is Y= F(K).
As usual, production is strictly increasing in the capital but subject to diminishing marginal productivity. So, we will think of the representative consumer as having the additional role of producer with direct access to this technology.
A unit of capital is created from a unit of the consumption good. What it means is capital is consumable, that is, after having been used to produce the output, it can be "eaten". Due to the presence of investment, now, the total domestic private wealth at the end of a period t would be B(t+1) + K(t+1), the sum of net foreign assets B(t+1) and the stock of domestic capital K(t+1).
The stock of capital K(t+1) accumulated through the end of period t is the sum of preexisting capital K(t) and new investment during period t, I(t) (ignoring depreciation of capital):


Finally, rearranging terms in this equation shows that the current account surplus is,

One way to interpret the preceding current account identity is to label national saving as S(t)

Thus we get an economy with investment,
National saving in excess of domestic capital formation flows into net foreign asset accumulation.
The saving-investment identity discloses that the current account is fundamentally an intertemporal phenomenon. The identity CA = S - I, is vital for analyzing how economic policies and disturbances change the current account. Will a protective tariff, often imposed to improve the current account, succeed in its aim? The answer depends on how the tariff affects saving and investment.
Another thing to be noted is that CA, S and I are jointly determined endogenous variables that respond to common exogenous shocks, it may be misleading to identify a specific ex-post investment or saving shift as the "cause" of a current account change.
The intertemporal budget constraint in the presence of investment term becomes,

Now it is the present value of consumption plus investment that is limited by the present value of output.
In this economy with investment, a representative individual maximizes U,

subject to budget constraint. To simplify further, observe that people will never wish to carry capital past the terminal period 2. Thus capital K2 accumulated in period 1 will be consumed at the end of period 2 and K2 will be zero implying that,

Thus the maximation equation transforms to,

The two corresponding first-order conditions obtained are,

An extra unit of output invested on date 1 can be fully consumed, together with its marginal contribution to output, F'(K2), on date 2. The 2nd first-order condition says that period 1 investment should continue to the point at which its marginal return is the same as that of a foreign loan. A critical feature is its implication that the desired capital stock is independent of domestic consumption preferences! Other things equal, wouldn't a less patient country, one with a lower value of beta, wish to invest less? Not necessarily, if it has access to perfect international capital markets. A country that can borrow abroad at the interest rate r never wishes to pass up investment opportunities that offer a net rate of return above r.
The production possibilities frontier is described by the equation,

The PPF's slope obtained by differentiation:

Capital's diminishing marginal productivity makes the PPF strictly concave as shown.
Point A is the autarky equilibrium. There, the PPF is tangent to the highest indifference curve the economy can reach without trade. The common slope of the two curves at A is -(1+r(a)).
If the economy faces a world interest rate, r, lower than the autarky rate r(a) implied by the dual tangency at point A. Thus, at A, the marginal domestic investment project offers a rate of return above the world cost of borrowing. The opportunity to trade across periods with foreigners lets domestic residents gain by investing more and producing at point B, through which the economy's new budget line passes. Production at B maximizes the present value of domestic output by placing the economy on the highest feasible budget line at world prices. Consuming at point C gives the economy the highest utility level it can afford.
The horizontal distance between A and B is the extra investment generated by opening the economy to the world capital market. The horizontal distance between A and C shows the extra first-period consumption that trade simultaneously allows. Since total first-period resources Y1+K1 haven't changed, the sum of two horizontal distances- the distance from B to C- is the first-period current account deficit.
The utility curve through point C lies above the one through point A. The distance between them measures the gains from trade. Trade gains were entirely due to smoothing the time path of consumption. There is an additional source of gain, the change in the economy's production point from A to B.
In this model, we assume that output is produced using capital, which, in turn, can be accumulated through investment. The production function for new output in either period is Y= F(K).
As usual, production is strictly increasing in the capital but subject to diminishing marginal productivity. So, we will think of the representative consumer as having the additional role of producer with direct access to this technology.
A unit of capital is created from a unit of the consumption good. What it means is capital is consumable, that is, after having been used to produce the output, it can be "eaten". Due to the presence of investment, now, the total domestic private wealth at the end of a period t would be B(t+1) + K(t+1), the sum of net foreign assets B(t+1) and the stock of domestic capital K(t+1).
The stock of capital K(t+1) accumulated through the end of period t is the sum of preexisting capital K(t) and new investment during period t, I(t) (ignoring depreciation of capital):

Next, the change in total domestic wealth, national saving, is

Thus we get an economy with investment,
National saving in excess of domestic capital formation flows into net foreign asset accumulation.
The saving-investment identity discloses that the current account is fundamentally an intertemporal phenomenon. The identity CA = S - I, is vital for analyzing how economic policies and disturbances change the current account. Will a protective tariff, often imposed to improve the current account, succeed in its aim? The answer depends on how the tariff affects saving and investment.
Another thing to be noted is that CA, S and I are jointly determined endogenous variables that respond to common exogenous shocks, it may be misleading to identify a specific ex-post investment or saving shift as the "cause" of a current account change.
The intertemporal budget constraint in the presence of investment term becomes,

Now it is the present value of consumption plus investment that is limited by the present value of output.
In this economy with investment, a representative individual maximizes U,

subject to budget constraint. To simplify further, observe that people will never wish to carry capital past the terminal period 2. Thus capital K2 accumulated in period 1 will be consumed at the end of period 2 and K2 will be zero implying that,

Thus the maximation equation transforms to,

The two corresponding first-order conditions obtained are,

An extra unit of output invested on date 1 can be fully consumed, together with its marginal contribution to output, F'(K2), on date 2. The 2nd first-order condition says that period 1 investment should continue to the point at which its marginal return is the same as that of a foreign loan. A critical feature is its implication that the desired capital stock is independent of domestic consumption preferences! Other things equal, wouldn't a less patient country, one with a lower value of beta, wish to invest less? Not necessarily, if it has access to perfect international capital markets. A country that can borrow abroad at the interest rate r never wishes to pass up investment opportunities that offer a net rate of return above r.
The production possibilities frontier is described by the equation,
The PPF's slope obtained by differentiation:

Point A is the autarky equilibrium. There, the PPF is tangent to the highest indifference curve the economy can reach without trade. The common slope of the two curves at A is -(1+r(a)).
If the economy faces a world interest rate, r, lower than the autarky rate r(a) implied by the dual tangency at point A. Thus, at A, the marginal domestic investment project offers a rate of return above the world cost of borrowing. The opportunity to trade across periods with foreigners lets domestic residents gain by investing more and producing at point B, through which the economy's new budget line passes. Production at B maximizes the present value of domestic output by placing the economy on the highest feasible budget line at world prices. Consuming at point C gives the economy the highest utility level it can afford.
The horizontal distance between A and B is the extra investment generated by opening the economy to the world capital market. The horizontal distance between A and C shows the extra first-period consumption that trade simultaneously allows. Since total first-period resources Y1+K1 haven't changed, the sum of two horizontal distances- the distance from B to C- is the first-period current account deficit.
The utility curve through point C lies above the one through point A. The distance between them measures the gains from trade. Trade gains were entirely due to smoothing the time path of consumption. There is an additional source of gain, the change in the economy's production point from A to B.
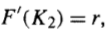

Comments
Post a Comment