2nd Generation Currency Crisis Model
where,
the target output is, y_tilda
It is different from the natural level of output which is, y_bar
From PPP we get,

Government has to suffer cost if it breaks the promise of maintaining the peg. It has adopted a "fixed but adjustable" exchange rate.
If it devalues than it suffers the cost of,

If it revalues than it suffers the cost of,

The economy is on the expectations-augmented Philips curve,
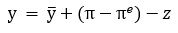
where z is the supply shock
The target output is above the natural rate of output given by,

How the model rolls?
1. Private agents form inflation expectations (pi_e)
2. Supply shock occurs (z)
3. The government then decides on the level of inflation for the economy (pi)
Had there been no cost term then the level of inflation rate chosen by the government would have been such that,
Had government not been able to change the exchange rates then,
Thus, in the absence of cost term, the government would always be better off by changing the exchange rates.
However, when cost term is introduced, then the government would suffer if it simply changes the exchange rates. Therefore, it will only choose to alter the exchange rates only when z is high enough,
Now, the private sector, as mentioned above, chooses depreciation expectations pi_e before observing either z or pi. In contrast, the government chooses pi after observing both z and pi. Also, the private sector knows the methodology with which the government makes its decisions. So, the rational expectations of inflation pi in the next period, given wage settlers expectations pi_e, is
Expected inflation pi_e enters here both in determining the inflation rate the government chooses conditional on choosing to realign and in determining the probability of a realignment. The fact that z depends on pi_e leads to non-linearity in equations.
For the shown distribution of z (uniform distribution of z over [-Z, Z]), we obtain,
Now, we know that z_upper_bar and z_lower_bar are functions of pi_e. So, as pi_e changes, z_upper_bar and z_lower_bar changes and so does the government's decision criteria of maintaining the exchange rates.
The equilibrium value of inflation expectations by agents would be at the point where
because of rational expectations. It can, therefore, be shown that inflation expectations calculated by agents follow a particular path and 3 equilibria points arise.
Point 1:


Point 3:

Having adopted a fixed but adjustable exchange rate, the government is powerless to enforce it's favoured low-inflation equilibrium at point 1. It may even end up being gamed into a free float (equilibrium 3), paying the fixed cost c_upper_bar with no benefit from having partially committed to a fixed rate. The root problem is that high expected depreciation in and of itself, by incipiently raising unemployment, creates an incentive for the government to validate expectations ex-post by devaluing.
With multiple equilibria some seemingly unimportant event could trigger an abrupt change in expectations, shifting the equilibrium from one in which only a very bad realization of z forces the government off the fixed rate to one in which even a relatively small z does so. Such an event would look much like the sudden speculative attacks on exchange rates we analyzed in 1st generation models. But here the situation is analogous to a bank run in which withdrawals sparked by depositor fears can themselves cause an otherwise viable bank to fail.
It is important to note that a government with strong fundamentals (e.g. c_upper_bar and chi large, k low) is less vulnerable to speculative attacks taking the form of a shift in equilibria.
ESSAY

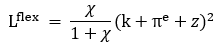


















Comments
Post a Comment