Intertemporal trade and Current Account balances (Model Without Investment)

One fundamental way open and closed economies differ is that an open economy can borrow resources from the rest of the world and lend them abroad. Such resource exchanges over time are called intertemporal trade. 

Much of the macroeconomic action in an open economy is connected with its intertemporal trade, which is measured by the current account of the balance of payments. The main goal here is to describe how a country can gain from rearranging the timing of its consumption through international borrowing and lending. 

Framework and Assumptions:
1. Small open economy
2. There is a single good. No distinction between foreign and domestic good.
3. Agents have perfect foresight.
4. Agents are identical and population size is unity
5. 2-period endowment economy

An individual "i" maximizes lifetime utility which depends on period consumption levels, denoted by c_i:

In this equation, beta is a fixed preference parameter, called the subjective discount or time-preference factor, that measures the individual's impatience to consume. 

We assume that the period utility function is u(c_i) is strictly increasing in consumption and strictly concave.

Let y_i denote the individual's output and r the real interest rate for borrowing or lending in the world capital market on date 1. Then consumption must be chosen subject to the lifetime budget constraint.

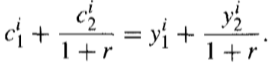
The constraint restricts the present value of consumption spending to equal the present value of output. The output is perishable and thus cannot be stored for later consumption.

We assume that the consumer bases decisions on perfect foresight of the future. Perfect foresight ensures that a model's predictions are driven by its intrinsic logic rather than by ad hoc and arbitrary assumptions about how people form expectations. Solving the problem of maximization subjected to lifetime budget constraint, the individual's optimization problem reduces to,

The first-order condition for this problem is:

which is called an intertemporal Euler equation. This Euler equation has a simple interpretation: at a utility maximum, the consumer cannot gain from feasible shits of consumption between periods. A one-unit reduction in first-period consumption, for example, lowers U by u'(c1_i). The consumption unit thus saved can be converted (bu lending it) into 1+r units of second-period consumption that raise U by (1+r)(beta)u'(c2_i).

An alternative interpretation closely resembles static price theory is suggested by writing it as:

The left-hand side is the consumer's marginal rate of substitution of the present (date 1) for future (date 2) consumption, while the right-hand side is the price of future consumption in terms of present consumption.

An individual "i's" optimal consumption plan is found by combining the first-order conditions with the inter-temporal budget constraint. The consumption behaviour depends on the value of beta that is, when the subjective time preference rate and the market interest rate differs, the motivation to smooth the consumption is modified y an incentive to tilt the consumption path:

1. If beta = 1/(1+r), then c1_i = c2_i

2. If beta > 1/(1+r), then c1_i < c2_i

3. If beta < 1/(1+r), then c1_i > c2_i

We assume that all individuals in the economy are identical and that the population size is 1. This assumption allows us to drop the individual superscript "i" and to identify per capita quantity variables with national aggregate quantities, which we denote by uppercase, non-superscripted letters. Thus, if C stands for the aggregate consumption and Y stands for aggregate output, the assumption of a homogeneous population os size 1 implies that c_i = C and y_i = Y for all individuals i. Our assumed demographics simplify the notion by making the representative individual's first order conditions to describe aggregate dynamic behaviour. The mentioned Euler equation, therefore, will also govern the motion of aggregate consumption.

Since the economy is small, the real interest rate r is exogenous. So, the small economy can carry out any inter-temporal exchange of consumption it desires at the given world interest rate r, subject only to its budget constraint. 

The idea of a representative national consumer, though a common device in modern macroeconomic modelling, may seem implausible. There are, however, three good reasons for taking the representative-consumer case as a starting point.

1. Several useful insights into the macroeconomy do not depend on a detailed consideration of household differences.

2. There are important cases when one can rigorously justify using the representative-agent model to describe aggregate behavior. 

3. Many models in international macroeconomics are interesting because they assume differences between residents of different countries, Sometimes the simplest way to focus on these cross-country differences is to downplay differences within countries.

Because international borrowing and lending are possible, there is no reason for an open economy's consumption to be closely tied to its current output. Country can import or export to adjust consumption and output gaps.

A country's current account balance over a period is the change in the value of its net claims on the rest of the world - the change in its net foreign assets. The current account balance is said to be in surplus if positive so that the economy as a whole is lending, and in deficit if negative so that the economy is borrowing. Remember, that a country with positive net exports must be acquiring foreign assets of value equal to the increase in exports because it is selling more to foreigners than it is buying from them. Balance of payments statistics records a country's net sale of assets to foreigners to foreigners under its capital account balance. Hence, the capital account surplus preceded by a minus sign - the net increase in foreign asset holdings - equals the current account balance.

To clarify the concept of the current account, let B(t+1) be the value of the economy's net foreign assets at the end of a period t. The current account balance over period t is defined as 

In general, the date t current account for a country with no capital accumulation or government spending is

Our formulation assumed that B1 = 0, making 

Also, we have assumed that the economy ends in period 2 holding no uncollected claims on foreigners, so B3 = 0. Thus, 

The figure below combines representative individual's indifference curves with the intertemporal budget constraint graphed as,

It provides a diagrammatic derivation of the small economy's equilibrium and the implied trajectory of its current account. The economy's optimal consumption choice is at point C, where the budget constraint is tangent to the highest attainable indifference curve. The first-period current account balance (a deficit here) is simply the horizontal distance between the date 1 output and consumption points. Similarly, the second-period current account balance (a surplus here) is the distance between the date 1 output and consumption points. Thus, the model suggests that an unbalanced current account is not necessarily a bad thing. For example, a country clearly does better running an unbalanced current account in both periods than it would if forced to set C1 = Y1 and C2 = Y2 (the autarky point A).

The factor that leads to some country running a current account deficit while others running a current account surplus lies in the difference between their autarky rates and the world real interest rates. Were the economy restricted to consume at the autarky point A, the only real interest rate consistent with the Euler equation would be the autarky interest rate r_a, as shown, 

So, when the latter autarky price is below the world relative price of future consumption, r_a > r, future consumption is relatively cheap in the home economy and present consumption is relatively expensive. Thus the home economy will import present consumption from abroad int he first period (running CA deficit) and export consumption later (by repaying its foreign debt). This result is in accord with the principle of comparative advantage from international trade theory, which states that countries tend to import those commodities whose autarky prices are high compared with world prices and export those whose autarky prices are comparatively low.

Existence of gains from intertemporal trade does not depend on the sign of the country's initial current account balance, as could be understood now. The reason is simple, however. What produces gains is the change to trade with someone different from oneself. Indeed, the greater the difference, the greater the gain. The only case of no gain is the one in which, coincidentally, it happens that r_a = r. 

This reasoning also explains how changes in world interest rates affect a country's welfare. The economy reaps trade gains by borrowing initially because its autarky interest rate is above the world rate, r. Notice, however, that, were the world interest rate even lower, the economy's welfare after trade would be higher (budget constraint flatter). The basic reason for this welfare gain is that a fall in the world interest rate accentuates the difference between the home country and the rest of the world, increasing the gains from trade.